Spatium vectoriale

Spatium vectoriale^[1] vel spatio lineare est collectio rerum vectorum appellatarum, quae inter se addi et per numeros scalares dictos multiplicari possunt. Scalares saepius sunt numeri reales, sed etiam sunt spatii vectorialia ubi multiplicatio scalaris numeris complexis, numeris rationalibus, aut quemlibet corpore fit.

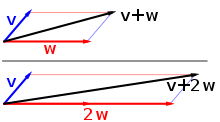
Rigorose, copia E (cum operationes + et •) structura spatii vectorialis super corpus commutativum K habet si:

(E , +) caterva abeliana est.
• distributivus associativusque est.
$1_{K}$ de • elementum neuter est.

Proprietates quae spatium vectoriale definiunt

Spatium vectoriale in $\mathbb {R}$ est copia $V$ , cui definiantur operationes summae $+:V^{2}\rightarrow V$ et multiplicatio scalaribus $\cdot :\mathbb {R} \times V\rightarrow V$ quae has proprietates satisfaciant:

$1v=v,0v={\underline {0}}$ , omnibus elementis copiae $V$ , quae hic littera $v$ designantur;
Summa est commutativa: $\forall v,w\in Vv+w=w+v$ ;
Est summae oppositum, quod est numerus qui vectori additus zerum producit: $\forall v\in V\exists -v\in V:v+(-v)=0$ ;
Est summae neutrum, quod est numerus qui vectori additus eum ipsum producit: $\exists 0\in V:\forall v\in Vv+0=v$ ;
Summa est associativa: $\forall u,v,w\in V:(u+v)+w=u+(v+w)$ ;
Multiplicatio scalaribus est associativa: $\forall \lambda ,\mu \in \mathbb {R} ,\forall v\in V(\lambda \mu )v=\lambda (\mu v)$ ;
Multiplicatio scalaribus est distributiva: $\forall \lambda \in \mathbb {R} ,\forall v,w\in V\lambda (v+w)=\lambda v+\lambda w{\text{ atque }}\forall \lambda ,\mu \in \mathbb {R} ,\forall v\in V(\lambda +\mu )v=\lambda v+\mu v$ .

Elementa spatii vectorialis vectores, summaeque neutrum vector nullus ${\underline {0}}$ appellantur.

Subspatium vectoriale

Spatiis vectorialibus sunt subcopiae quae similes sunt lineis apud subcopias spatii euclidei. Hae subcopiae sunt subspatia vectorialia, quae subcopiae sunt spatii vectorialis clausae multiplicationi scalaribus summaeque:

$W\subseteq V:\forall w,w_{1},w_{2}\in W,\forall \lambda \in \mathbb {R} \rightarrow w_{1}+w_{2}\in W,\lambda w\in W$

Vector nullus versatur in omnibus subspatiis vectorialibus, quia si $w$ est vector in subspatio, etiam est $0w={\underline {0}}$ (zerum est scalar). Et quod unus negativus est scalar quoque, si subspatio vectoriali inest vector, etiam eius oppositus inest.

In secundis, omnia subspatia vectorialia sunt spatia vectorialia, spatiaque vectorialia sunt subspatia vectorialia ipsorum. Etiam copia solius vectoris nullius $\{{\underline {0}}\}$ est subspatium vectoriale.

Spatia vectorialia in systematibus aequationum solvendis

In systema aequationum lineare, si dextrae signi aequationis $=$ instant sola zera, sicque videtur:

$Ax={\underline {0}}$

Id systema homogeneum dicitur.

Demonstrari potest, si $W\subseteq \mathbb {R} ^{n}$ est copia solutionum systematis linearis homogenei numero $n$ variabilium ignotarum scripti ut $Ax={\underline {0}}$ , $W$ esse subspatium vectoriale spatii $\mathbb {R} ^{n}$ . Idem si non est homogeneum systema, eius solutiones non sunt subspatium, quod non inest vector nullus.

$W$ ut subspatium vectoriale

Systema enim sic videtur:

Executare non potest (MathML: Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/la.wikipedia.org/v1/":): {\displaystyle \biggl\{\begin{matrix}a_{11}x_1+...+a_{1n}x_n=0\\...\\a_{m1}x_1+...+a_{mn}x_n=0\end{matrix}}

Si vectores ${\underline {v}},{\underline {w}}$ solutiones sunt, id igitur verum est:

${\biggl \{}{\begin{matrix}a_{11}v_{1}+...+a_{1n}v_{n}=0\\...\\a_{m1}v_{1}+...+a_{mn}v_{n}=0\end{matrix}}{\biggl \{}{\begin{matrix}a_{11}w_{1}+...+a_{1n}w_{n}=0\\...\\a_{m1}w_{1}+...+a_{mn}w_{n}=0\end{matrix}}$

Si dua systema summantur, vel scalari multiplicantur, id patet:

${\biggl \{}{\begin{matrix}a_{11}(v_{1}+w_{1})+...+a_{1n}(v_{n}+w_{n})=0\\...\\a_{m1}(v_{1}+w_{1})+...+a_{mn}(v_{n}+w_{n})=0\end{matrix}}{\biggl \{}{\begin{matrix}a_{11}(\lambda v_{1})+...+a_{1n}(\lambda v_{n})=0\\...\\a_{m1}(\lambda v_{1})+...+a_{mn}(\lambda v_{n})=0\end{matrix}}$

Summa igitur solutionum et multiplicatio sunt solutio ipsius systematis, quod est definitio subspatii vectorialis (clausi summae multiplicationique).

Notae

↑ Isabel Schlangen, Drei Quanten-sl₂-Verallgemeinerungen des gefärbten Jonespolynoms in zwei Parametern (dissertatiuncula, Rheinischen Friedrich-Wilhelms-Universität Bonn, 2012), vi.

Bibliographia

Abate, De Fabritiis, 2015. Geometria analitica con elementi di algebra lineare. McGraw Hill Education. ISBN 9788838615146.

Nexus interni

[1] Isabel Schlangen, Drei Quanten-sl₂-Verallgemeinerungen des gefärbten Jonespolynoms in zwei Parametern (dissertatiuncula, Rheinischen Friedrich-Wilhelms-Universität Bonn, 2012), vi.

[1]