Tensor (mathematica)

Tensor est objectus geometricus qui combinet spatium vectoriale, constantes, et alteros tensores in modo lineari. Notio plus generalis est quam vector vel matrix. Tensor indices habet, qui similes sunt dimensionibus.

Tensor ordinis alteris cuius basis est (e₁, e₂, e₃)

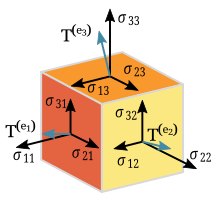
Multiplicatio scalaris vectorum (productum puncto notatum), quae scalarem e duobus vel pluribus vectoribus facit, est tensor simplicissimus.

Tensores sunt magni momenti in physica.

Bibliographia

• Donald Danielson. Vectors and Tensors in Engineering and Physics. Novi Eboraci: Perseus, 2003.
• Ferrante Neri, Linear Algebra for Computational Sciences and Engineering. Helvetia: Springer, 2016.
• Bernard Schutz. Geometrical Methods of Mathematical Physics. Cantabridgiae: 1980.
• C. E. Weatherburn, Elementary Vector Analysis, with Applications to Geometry and Physics. Londini: G. Bell & sons, 1935.

Nexus externi

Vicimedia Communia plura habent quae ad tensorem spectant (Tensor, Tensors).

• Tensor apud MathWorld

Haec stipula ad mathematicam spectat. Amplifica, si potes!