Medietas
Valor medius exspectatus, vel medietas,[1] in statistica est numerus quo distributiones statisticae singulo effinguntur valore. Cuius signum usitatum μ (mu) est.
Exempli gratia, si habes copiam numerorum (2, 4, 6, 8, 10), medius horum numerorum valor arithmeticus est (2 + 4 + 6 + 8 + 10)/5 = 6. Sed si copia est (2, 3, 4, 6, 20), μ = 7, et si copia est (1, 1, 6, 7, 7), μ = 4.4.
Plus exacte, valor medius exspectatus est primum momentum centrale distributionis probabilisticae, cum medietas apud subcopiam exemplorum e populatione extractam computetur.
Alicubi in re mathematica habemus alios valores medios: valor medius arithmeticus, valor medius geometricus, valor medius harmonicus; magnitudo centralis est notio similis.
Multa sunt genera medietatum, quae ita subdividi solent:
- Medietates analyticae eae appellantur, quae adhibendis operationibus computentur cunctis characteris valoribus consideratae distributionis;
- Medietates laxae, ad quas computandas soli subcopiae valorum operationes illae adhibentur. In eis insunt medietates positionis, tamquam mediana et quantilia.
Exempli gratia, medietas arithmetica analytica est, sed quantile est laxum. Cum solorum characterum quantitativorum distributionibus analyticae adhibeantur medietates, medietatibus positionis etiam characteribus qualitativis ordinatis utimur.
Ad definendam medietatem ratio
recensereDuae usitatae sunt rationes, quibus functionem appellari medietatem constituimus.
Prima est ratio chisiniana, qua medietas est functio quae, cum ipsa adhibita sit copiae exemplorum cardinalitate N, eundem producat valorem M, quasi adhibeatur ipsa ad aliam copiam N-ies complectentem valorem M:
Secunda est ratio minimae amissionis, qua medietas est numerus quo functio amissionis quaedam minima sit. Exempli gratia, dicamus esse amissionem formulam , ubi littera M medietatem inveniendam significat: constat minimam esse amissionem, cum littera M valorem medium arithmeticum significet.
Medietas arithmetica
recensereMedietas arithmetica, quae usitatissima ac notissima ex omnibus statisticis rebus est, ita definitur:
Verbis posse dici medietatem arithmeticam esse elementorum valorum summam, in numerum N partium divisam (ubi, ut clarum est, numerus N est cardinalitas copiae elementorum).
Non modo medietas arithmetica in numerum unum exempla cohibens proficit, sed etiam iuvat ut aliae res statisticae definiantur, tamquam indices varietatis.
Pariter ita definitur differentia elementi a medietate arithmetica: .
Proprietates medietatis arithmeticae
recensere- Medietas arithmetica inter extrema comprehenditur cuiusque distributionis: numeris scriptu, si est elementum in loco i-esimo distributionis ordinatae, . In extrema vero incidit, si ipsa duo aequalia sunt, ergo si aequale est quidque elementum. Omnia enim elementa inter minimum maximumque comprehenduntur, , ergo , e quo thesim ducimus.
- Summa elementorum est N-upla medietas arithmetica. Chisinianam igitur rationem explet: . Id confestim ex definitione medietatis arithmeticae excipimus, cum duo membra N-upla fecerimus.
- Summa omnium differentiarum a medietate arithmetica nulla est: .
- Summa differentiarum elementorum a numero quodam c ad secundam potentiam dignatarum, minima fit si ipse est medietas arithmetica: . Ob eam dici rem potest, melius medietatem hanc elementa effigere, cum sit eius "distantia" ab eis minima, quod minimae amissionis rationem explet. Ad id demonstrandum explicemus functionem: , et cum summatoria a pedice non dependat, scribi potest: ob proprietatem tertiam supradictam, quod erat demonstrandum.
- Linearitas: si nova elementa fiunt, appellata signo medietate elementorum , medietas arithmetica elementorum ita computatur: . Ex quo consequitur ut medietas etiam sit translativa, quia cum numerus a quoque elemento subtractus sit, sic a medietate isdem numerus est subtrahendus; atque homogenea, quia quotiens elementa multiplicentur, totiens medietas multiplicanda est.
- Associativitas: si est numerus L copiarum quarundam cardinalitatibus medietatibusque , ipsarum unionis medietas ita computatur: . Itaque cum subcopiarum medietates solarum cognoscantur, copiae medietas potest duci.
Medietas harmonica
recensereCasibus quibusdam, non oportet medietate arithmetica uti.
Exempli gratia, sit autocinetum quod spatium quinquaginta chiliometrorum bis transivit, primum hora octogenis chilometris, secundum quadragenis. Tametsi arithmetica est medietas sexagena chilometra hora, amplius oportet medietatem computare, spatium totale dividendo transitum tempore totali consumpto:
Cum sciamus velocitatem significare quotiens sit tempus transitionis in spatio transito (v=s/t), ita quoque id scribi potest:
quod patet haud aequale medietati arithmeticae.
Rite igitur sic definitur medietas harmonica:
Proprietates medietatis harmonicae
recensere- Ut medietas arithmetica, inter extrema comprehenditur distributionis cuiusque: . Elementa enim reciproca sunt minora minimo reciproco maioraque maximo reciproco: , ergo .
- Ratio Chisiniana expletur: elementorum enim reciprocorum summa aequalis est eorum cardinalitati medietate harmonica divisae: .
- Homogeneitas: quicque elementum si -uplum fit, cum numerus nullus non sit, medietas harmonica nova in -uplam medietatem priorem commutatur: .
- Associativitas: cum subcopiarum quarundam medietates harmonicae cognoscantur, illarum unionis medietas harmonica ita computari potest: .
Medietas geometrica
recensereCasus alius quo uti medietate arithmetica non oportet, ille est, quo elementa non magnitudem rerum effingunt, sed mutationes earum.
Exempli gratia, sit summa pecuniae, cui post annum unum decimum (initii summa 110% fit) additum erit, anno secundo dimidium (primi anni summa fit 150%), anno tertio quartum (secundi anni summa fit 125%). Medietas multiplicationis anni unius non est medietas arithmetica ; si esset, tum haberetur post annum tertium . Quare oportet medietate geometrica uti, quae sic definitur:
quod est -esima radix elementorum inter ipsa multiplicatorum.
Proprietates medietatis geometricae
recensere- Ut medietates arithmetica atque harmonica, inter extrema comprehenditur distributionis: , quod demonstratur ut aliis medietatibus.
- Expletur ratio Chisiniana: elementa enim multiplicata aequalia sunt dignatae ad N-esimam potentiam medietati geometricae: .
- Homogeneitas: quicque elementum si -uplum fit, cum sit numerus positivus, sic medietas geometrica -upla est facienda, quod enim facile sic demonstratur: .
- Logarithmus medietatis geometricae est medietas arithmetica logarithmorum elementorum: . Ex eo consequitur ut ipsa medietas etiam sic scribi possit: .
- Associativitas: eadem notatione ac priorum medietatum, .
Medietas quadratica
recensereMedietas ista praecipue adhibetur cum omnia elementa positiva facere oporteat.
Rite ita definitur: , quod est radix quadrata medietatis arithmetica elementorum ad secundam potentiam dignatorum.
Ut priores medietates, medietas quadratica inter extrema comprehenditur, rationem chisinianam explet ( ), atque est homogenea et associativa ( ).
Medietates potentiae
recensereSupradictae medietates (arithmetica, harmonica, geometrica, quadratica) omnes una classe medietatum cohibentur, quae medietates potentiae appellantur. Rite dicitur medietas potentiae r-esimi ordinis sic definiri:
Ita patet esse medietatem potentiae secundi ordinis medietatem quadraticam, primi ordinis arithmeticam, negativi primi ordinis harmonicam.
Aliud quoque demonstrari potest, quod limite numeri ad infinitatem negativam fit medietas potentiae valor minimus ( ), ad zerum medietas geometrica ( ), ad infinitatem positivam valor maximus ( ).
Etiam demostratum esse in numero medietatem potentiae functionem crescentem, ita ut:
ex quo patet omnes medietates potentiae inter elementum minimum maximumque comprehendi, et istum medietatum supra descriptarum esse ordinem:
Medietates analyticae distributionibus frequentiarum
recensereDistributionibus frequentiarum adhibendae medietates supradictae parum mutantur ea ratione, quod si cui valori est frequentia quaedam, necesse est habere numerum elementorum eo valore huic frequentiae aequalem. Exempli gratia, si distributioni inscriptum est valori "2" esse frequentiam "3" et valori "4" frequentiam "2", constat adesse quinque elementa, quibus medietas computanda est: .
Itaque, appellata signo frequentia valoris , cum sit numerus valorum, ita supradictae medietates computantur:
vel
Medietates distributionum in classes subdivisarum
recensereSi frequentiae in classes subdivisae sunt, singulae medietates arithmeticae elementorum cuiusque classis computandae sunt. Exempli gratia, si classis prima est ac secunda , insuntque primae elementa secundaeque , primae classi est medietas 2 secundaeque 8. Si numerum habemus classium appellamusque signo medietatem classis , quaevis medietates possunt computari cuiusvis distributionis in classes subdivisae, cum in valorum locum medietates subdantur classium. Itaque fit media arithmetica:
Priore igitur in exemplo medietas est: .
Classium autem medietates cum saepe non cognoscamus, quia solis valoribus subdivisis distributio praebita sit, licet in medietatum locum subdere eius classis valor centralis: , appellatis signis et classis extremis. Videtur tamen is valor centralis aequalis esse classis medietati, si uniformiter elementa in classem distribuuntur. Eadem enim differentia elementis interposita, tamquam , id statim liquet: .
Medietates analyticae ponderatae
recensereAliquando medietas est computanda copiae elementorum, quae non omnia aequaliter gravia sunt vel nostra intersunt. Si exempli gratia homines quidam tres examinationes subeunt, primaque est gravissima trium, non oportet medietate arithmetica uti ut soletur, at pondus maius quoddam primae examinationi imponere.
Appellemus pondera illa signis , quae sint numero , eorumque summam littera . Tum medietas arithmetica ponderata sic definitur:
Ea medietate eaedem proprietates valent et medietate arithmetica simplici, cum in locum valorum subdatur eorum multiplicatio cum ponderibus. Ita etiam patet medietatem distributionis frequentiarum inter medietates ponderatas comprehendi, cum pondera frequentiae sint: .
Aliae medietates sic transferuntur:
Mediana
recensereMediana est potissima inter medietates laxas. Ei computandae, necesse est distributionis elementa ordinari.
Si est distributio ordinata , sic rite mediana definitur:
vel verbis, elementum centrale distributionis ordinatae si N impar est, medietasque arithmeticae duorum elementorum centralium si N par est; mediana enim in duas partes distributionem dividit.
Inter eius proprietates:
- Mediana quoque inter extrema comprehenditur ut medietates analyticae supradictae;
- Est linearis ut medietas arithmetica; impar enim si N est, mediana uni elemento aequalis, cui additionem multiplicationemve adhibitam patet et medianae adhibendam; ac si par est, mediana est medietas arithmetica quaedam, quam scitur linearem.
- Ad eas id accedit, quod mediana amissionem absolutam minimam facit: si in locum litterae hic subditur mediana , minimus est iste numerus:
Ad tertiam proprietatem demonstrandam, sint elementa ordinata et quodlibet punctum , a quo amotionum absolutarum summa (amissio absoluta) est: .
Nunc si N est par, haec summa ita potest rescribi: , minima igitur est puncto inter omnes binos : . Quam condicionem satisfacit mediana.
Idem viget N impari, quod superior summa plane fit: , quae rursus minima fit puncto medianae aequali.
Quantilia empirica
recensereQuantilia (empirica) dici possunt medianam expandere, ut non modo in duas partes elementa aeque magnas distribui possint, sed etiam in tres, quattuor, decem, vel in quemcumque partium numerum ea velimus subdividere.
Rite, computando -ili -esimo copiae elementorum, ubi litteris et designentur numerus partium efficiendarum et quod quantile inter illa effecta producendum sit, huic formulae aptum numerum quaerimus:
Si membrum centrale huius disaequationis exacte aequale est primo, tunc quantile est ista medietas arithmetica:
Nisi est, simpliciter producitur elementum .
Exempli gratia, sit distributio ; tum si quartile primum quaeramus, istam aequationem solvamus: , cuius cum solutio sit , quartile primum est ; si autem primum quaeramus tertile, fit aequatio , solutione : tertile igitur est .
Patet medianam inter quantilia comprehendi, cum elementa in solas duas partes subdividantur ( ).
Facile quantilia ad frequentiarum distributiones adaptantur: sola disaequatione priore subduntur in locum membrorum et frequentiae cumulatae atque .
Quantilia distributionum frequentiarum in classes subdivisarum
recensereDifficilius autem est ut quantilia computemus, cum frequentiarum distributio in classes subdividerimus. Hic primum explicabimus, quomodo computetur mediana et postea alia quantilia.
Ad medianam adipiscendam, primum computanda classis mediana est, classis cui inest elementum medianum. Exempli gratia, sit haec distributio:
| Classis | [0,10) | [10,20) | [20,30] |
|---|---|---|---|
| Frequentia | 3 | 10 | 2 |
Amplissime liquet medianam esse, si sunt viginti et quinque elementa ordinata, elementum tertium decimum; quod id secundae classis valoribus [10,20) instat, ipsa est classis mediana.
Nunc ita appellemus classis medianae extrema: . Si ultro verum id habemus, quod elementa in classe mediana uniformiter distribuantur, potest sic medianam definiri:
Idque finaliter ad omnia quantilia adhiberi potest, cum pro fractione supponatur ea , neque inferatur classis mediana, sed classis cui -ile -esimum instat.
Aliae medietates laxae
recensereValor centralis
recensereMinime medietas arithmetica valori centrali confundere decet, qui sola est medietas arithmetica extremorum distributionis, vel rite:
Is valor tamen medietati arithmeticae competit, cum distributionis cuncta elementa ordinata inter se differant eandemque distantiam inter se habeant.
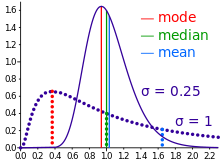
Moda
recensereModa valor est distributione frequentiarum, cuius maxima est frequentia, vel alterna vice, qui maximo est numero elementorum; cum distributio in classes subdivisa sit, maxima frequentia classis classis modalis appellatur.
Medietatum corroboramentum
recensereCum distributio statistica aliquando comprehendat valores abnormes vel anomalos, medietatibus analyticis uti non oportet sicut sunt, sed eas abnormalibus adaptari ad medietates robustas.
Adaptari solet medietas arithmetica in duas medietates novas, medietatem excisam et medietatem excisam cum substitutionibus.
Medietati excisae computandae, simpliciter capitur medietas arithmetica cunctorum elementorum, excepto numero quodam minimorum maximorumque. Exempli gratia, si distributio est , medietas 1-excisa est: , quod primum elementum minimum primumque maximum excepta sunt.
Rite ita scribi potest medietas k-excisa:
Medietas excisa cum substitutionibus
recensereIsti medietati computandae non excipiuntur elementa extrema, sed in eorum locum interiora elementa substituuntur, demum in minimorum locum quam ea maiora elementa proxima, in maximorum locum quam ea minora.
Exempli gratia, sit denuo distributio : tum medietate 1-excisa cum substitutionibus, minimum elementum excipitur et secundum additur, maximumque excipitur et additur quartum: . Rite:
Medietates laxae robustae
recensereCum etiam mediana videtur medietas robusta, sunt aliae duae, per quartilia computatae, quibus uti possumus, ita definitae:
ubi littera k-esimum quartile significat.
Utendae delectus medietatis
recensereCum pateat esse medietatem arithmeticam usitatissimam inter omnes, eaque oportere uti plerisque casibus nisi liqueat aliam medietatem magis praestare, ipsa aliquando non aptior est. Exempli gratia, si volumus medietatem elementorum reciprocorum computare, magis idonea medietas harmonica est; ac elementis quae mutationem rei significent, decet medietas geometrica. Aliter hac uti oportet, cum abnormales putantur inesse valores distributioni, quod hanc minus abnormalia afficiunt, vel cum logarithmi elementorum distributionem normalem efficiant, quare saepe ipsa biologi oecologique utuntur. Cum non omnia elementa aeque gravia sunt, saepe medietates haec ponderatas efficiuntur.
Parum medietas quadratica investigationibus prodest, sed saepe ex ipsa definiuntur alii indices statistici ut deviatio canonica.
Medietates positionis autem saepe prosunt cum valores abnormales distributioni insint. Exempli gratia ponamus tres has distributiones:
His eadem mediana est, quamquam trium singula medietas arithmetica mutatur. Denique saepe moda utimur, quod sola inter medietates computari potest, si character qualitativus est neque ordinatus.
Notae
recensere- ↑ https://www.tuttoenumero.it/wp-content/uploads/2013/12/Boethius-DeInstitutioneArithmetica.pdf, e Boethii de arithmetica libro primo, pagina quarta, capite septimo: ut si ponat quis quinarium numerum, altrinsecus circa ipsum sunt, supra quattuor, inferius sex. Hi ergo si iuncti sunt, faciunt decem, quorum quinque numerus medietas est.
Bibliographia
recensere- Cicchitelli, D'Urso, Minozzo. 2018. Statistica: principi e metodi. Pearson. ISBN 9788891902788.